Éléments de logique

Les connecteurs logiques sont les éléments du langages utilisés pour relier les propositions.

Implication	SI... ALORS IF... THEN	p ⇒ q p entraîne q	Table de vérité Diagramme de Venn
Équivalence	SI ET SEULEMENT SI	p ⇔ q p est équivalent à q	Table de vérité Diagramme de Venn
Conjonction & .	ET AND	p ∧ q p et q	Table de vérité Diagramme de Venn
Disjonction \|	OU OR	p ∨ q p ou q	Table de vérité Diagramme de Venn
Disjonction exclusive	OU exclusif XOR	p ⊕ q p ou q	Table de vérité Diagramme de Venn
Négation	NON NOT	¬p	Table de vérité Diagramme de Venn
Contradiction		p ∧ ¬p p et non-p	Table de vérité Diagramme de Venn
Tautologie		p ∨ ¬p p ou non-p	Table de vérité Diagramme de Venn

Diagramme de Venn et table de vérité

Les quantificateurs sont utilisés pour formuler les propositions dans la logique des prédicats. (les virgules favorisent la lecture).

Existence	Il existe au moins un...	∃ x, P(x) Au moins un x possède la propriété P
Unicité	Il existe un seul...	∃! x, P(x) Un seul x possède la propriété P
Universalité	Pour tout... Quel que soit...	∀ x, P(x) Tout x possède la propriété P
Composition ,	∀ x, ∃ y, P(x,y) Pour chaque x, il existe un y, qui satisfait P	∀ x, ∃ y, x > y (Vrai) Quel que soit x, il existe un y plus petit que lui
Composition ,	∃ x, ∀ y, P(x,y) Il existe un x qui, quel que soit y, satisfait P	∃ x, ∀ y, x > y (Faux) Il existe un x plus grand que tous les y
Négation de l'existence	¬(∃ x, P(x))	∀ x, ¬P(x) Tout x ne possède pas la propriété P
Négation de l'universalité	¬(∀ x, P(x))	∃ x, ¬P(x) Au moins un x ne possède pas la propriété P
Négation de composition	¬(∀ x, ∃ y, P(x,y)) ∃ x, ¬(∃ y, P(x,y)) ∃ x, ∀ y, ¬P(x,y)	¬(∃ x, ∀ y, P(x,y)) ∀ x, ¬(∀ y, P(x,y)) ∀ x, ∃ y, ¬P(x,y)

Remarque : Écriture simplifiée

En remplaçant ou (∨) par +, et (∧) par ., non (¬) par "surligné", Vrai par 1, Faux par 0, on obtient une écriture plus concise mais moins explicite.

(p + q) = p . q pour ¬(p ∨ q) = ¬p ∧ ¬q

a . 0 = 0 ; a . 1 = a ; a . a = a ; a . a = 0

a + 0 = a ; a + 1 = 1 ; a + a = a ; a + a = 1

La "Grammaire" de la logique des prédicats est constituée par :

- des variables notées x, y, z, x1, x2...

- des constantes notées a, b, c...

- des fonctions d'un ou plusieurs arguments notées f, g...

- des prédicats d'un ou plusieurs arguments notés p, q, r...

Un terme est une constante ou une variable ou une fonction.	terme = constante \| variable \| fonction "(" terme { "," terme } ")"
Un atome est constitué d'un prédicat d'un ou plusieurs termes.	atome = prédicat "(" terme { "," terme } ")"
Une formule est un atome ou une formule accompagnée d'un quantificateur ou la négation d'une formule ou deux formules liées par un connecteur.	connecteur = ∧ \| ∨ \| ⇒ \| ⇔ formule = atome \| ∀ variable formule \| ∃ variable formule \| ¬ formule \| formule connecteur formule

Formules équivalentes

Double négation.	¬ ¬ p	p
Idempotence.	p ∧ p	p
Idempotence.	p ∨ p	p
Absorption.	p ∧ ( p ∨ q )	p
Absorption.	p ∨ ( p ∧ q )	p
Commutativité du ∧.	p ∧ q	q ∧ p
Commutativité du ∨.	p ∨ q	q ∨ p
Associativité du ∧.	(p ∧ q) ∧ r	p ∧ (a ∧ r)
Associativité du ∨.	(p ∨ q) ∨ r	p ∨ (q ∨ r)
Distributivité du ∧ sur le ∨ (à gauche et à droite).	p ∧ (q ∨ r)	(p ∧ q) ∨ (p ∧ r)
Distributivité du ∨ sur le ∧ (à gauche et à droite).	p ∨ (q ∧ r)	(p ∨ q) ∧ (p ∨ r)
Loi de Morgan.	¬ (p ∨ q)	¬ p ∧ ¬ q
Loi de Morgan.	¬ (p ∧ q)	¬ p ∨ ¬ q
Implication.	p ⇒ q	¬ p ∨ q
Contraposition.	p ⇒ q	¬ q ⇒ ¬ p
Equivalence.	p ⇔ q	(p ⇒ q) ∧ (q ⇒ p)
Equivalence.	p ⇔ q	(p ∧ q) ∨ (¬ p ∧ ¬ q)

Métalangage

Le métalangage est le langage dans lequel on décrit les propriétés d'une théorie.

Le langage-objet est le langage dans lequel elle s'écrit.

Conséquence logique A1, A2, A3 B A signifie que A est une tautologie.	La conclusion B est vraie si les prémisses/hypothèses A sont vraies. Si A B est une tautologie (si A vrai alors B vrai) alors A B
Equivalence logique A B (p ⇒ q) (¬p ∨ q)	Les formules A et B ont la même valeur de vérité. Si A B est une tautologie alors A B
Inférence/Séquents A1, A2, A3 B1, B2, B3 A signifie que A est un thorème/un axiome.	Les A sont les prémisses/hypothèses et les B les conclusions de l'inférence. En langage formel : A1 ∧ A2 ∧ A3 ⇒ B1 ∨ B2 ∨ B3
Formule consistante ou satisfiable	Il existe (au moins) une interprétation de ses propositions pour laquelle elle est vraie.
Formule inconsistante	Fausse pour toutes les interprétations.
Formule valide	Vraie pour toutes les interprétations (tautologie, théorème)
Formule invalide	Il existe (au moins) une interprétation de ses propositions pour laquelle elle est fausse.
p ∧ q	consistante car si p vrai, q vrai / (p et q) vrai
p ∧ ¬ p	inconsistante car : (p et non p) toujours faux
p ∨ ¬ p	valide car (p vrai ou p faux) est toujours vrai
p ∨ q	invalide car si p faux, q faux / (p ou q) faux
Forme normale conjonctive	On appelle littéral une formule atomique ou une négation de formule atomique. Une clause est une disjonction de littéraux. Une formule est sous une FNC si elle est une conjonction de clauses.

Le principe de Non-Contradiction (en logique) affirme qu'une proposition ne peut pas être, au même moment, vraie et fausse, démontrable et réfutable.
Il est posé par Aristote comme une vérité première et une nécessité absolue. Une chose ne peut pas être et ne pas être en même temps. p n'est pas non p.

Soit p la proposition « Tous les hommes sont mortels »

p ∧ ¬ p n'a pas de sens « Tous les hommes sont mortels et Il existe des hommes qui ne sont pas mortels »

Sa contradiction est une tautologie :

¬ ( p ∧ ¬ p) ou

( ¬ p ∨ ¬ ¬ p) ( Loi de Morgan )

D'où, en logique classique, le principe du Tiers Exclu

( ¬ p ∨ p) ( avec ¬ ¬ p = p ). Une proposition ne peut être que vraie ou fausse.

Il n'y a pas de troisième voie.

∀a,b ∈ ℜ, ab = 0 ⇒ ( a = 0 ou b = 0 ). Si un produit est nul alors un des facteurs est nul

Soit p la proposition « a = 0 »

p ⇒ ( ab = 0 ) et ( p ou b = 0 )

¬ p ⇒ ( ab = 0 et a ≠ 0 ) ⇒ b = 0. On a encore ( ab = 0 ) et ( p ou b = 0 )

Il n'y a pas d'autre cas à envisager.

En logique intuitionniste le Tiers Exclu n'est pas un principe ( ¬ ¬ p signifie que p n'est pas contradictoire mais pas que p est vrai.

En revanche p ⇒ ¬ ¬ p
Remarque : la non contradiction est nécessaire aux juristes (coupable/non coupable) et aux mathématiciens (vrai/faux) mais elle ne satisfait pas totalement les physiciens quantiques (dualité onde/corpuscule).

L'implication
« Si tu as une bonne note tu auras un cadeau »
L'implication est utilisée dans le langage courant. C'est pourtant un concept mathématique déroutant qui n'apparaît pas identique selon l'angle sous lequel on le regarde.

Point de vue ensembliste

Soit A un ensemble d'objets qui vérifient la propriété p

Soit B un ensemble d'objets qui vérifient la propriété q

L'implication de q par p ( p ⇒ q ) est équivalente à l'inclusion de A dans B ( A ⊃ B ).
Cette approche n'est guère utile lorsque les propositions ne sont pas de même nature ou se réfèrent à un ensemble difficile à représenter « S'il pleut, j'irai au cinéma »

Point de vue de la logique formelle

p	q	p ⇒ q
V	V	V
V	F	F
F	V	V
F	F	V

⇒ (implication matérielle) est un connecteur c'est à dire une opération qui transforme deux propositions en une nouvelle proposition.

La valeur de vérité de (p ⇒ q) ne dépend que de celles de p et q (en accord avec sa table de vérité) et pas de leur contenu.
Cette approche permet de traiter toutes les propositions mais le cas de la prémisse fausse n'est pas conforme à la logique naturelle.

Point de vue du raisonnement déductif

Il s'agit de raisonnements de la forme

p est vraie

(p ⇒ q) est vraie

Donc q est vraie

qui mettent bien en évidence la différence de niveau entre une implication « si p alors q » et une déduction « donc q »
Cette approche ne fait appel qu'à des implications dont la premisse est vraie. D'autre part, la formulation semble établir un lien de causalité entre p et q.

L'Implication en logique classique ( Tiers exclu )

Notation. Définition. Contraposée

L'implication peut être représentée par un des symboles ⇒ → ⊃.

(p ⇒ q) se lit p entraine q ou p seulement si q ou encore si p alors q (pas donc).

Les formules ¬(p ∧ ¬q) soit (¬p ∨ q) décrivent la table de vérité de (p ⇒ q). Elles peuvent être prises comme définition.

De même (p ⇒ q) et (¬q ⇒ ¬p) ont la même table de vérité. Elles sont équivalentes et sont dites contraposées.

Cas de la prémisse fausse

Si p est faux, (p ⇒ q) est vraie quelle que soit la valeur de vérité de q.

Ce "choix", qui paraît artificiel n'est pourtant pas arbitraire.

p	q	p ⇒ q	¬q	¬p	¬q ⇒ ¬p
V	V	V	F	F	?1
V	F	F	V	F	F
F	V	?2	F	V	?2
F	F	?1	V	V	V

L'équivalence des contraposées
conduit à ?1 = V (lignes 2 et 5).

p	q	p ⇒ q	q ⇒ p
V	V	V	V
V	F	F	?2
F	V	?2	F
F	F	V	V

Si ?2 = F
p et q ne sont pas différenciées.
Les valeurs de p ⇒ q et q ⇒ p sont les mêmes, ce qui n'est vrai que pour l'équivalence.
Il faut donc que ?2 = V.

Propriétés de l'implication en logique classique (quels que soient p, q, r)

p ⇒ p - (d'après la réflexivité de la déduction)

p ⇒ (q ⇒ p) - (un des paradoxes de l'implication)

(¬p ⇒ p) ⇒ p - (raisonnement par l'absurde)

¬p ⇒ (p ⇒ q) - (principe d'explosion)

(p ⇒ q) ⇒ ((q ⇒ r) ⇒ (p ⇒ r)) - (d'après la transitivité de la déduction)

p ⇒ q équivaut à ¬(p ∧ ¬q) équivaut à ¬p ∨ q - (définition)

p ⇒ q équivaut à ¬q ⇒ ¬p - (contraposées)

p ⇒ (q ∧ r) équivaut à (p ⇒ q) ∧ (p ⇒ r) - (distributivité à gauche sur la conjonction)

p ⇒ (q ∨ r) équivaut à (p ⇒ q) ∨ (p ⇒ r) - (distributivité à gauche sur la disjonction)

Les paradoxes de l'implication (quels que soient p, q, r)
Un certain nombre de formules de la logique classique sont vraies mais ne tombent pas sous le (bon) sens.

Quelques formulations surprenantes

(¬p ∧ p) ⇒ q. Paradoxe de l'implication. De l'affirmation d'une contradiction on peut déduire n'importe quoi. (1).

q ⇒ (p ⇒ q). Le vrai découle de n'importe quoi.
« (il fait beau) alors (si (les poules ont des dents) alors (il fait beau)) » est vraie mais aussi « (il fait beau) alors (si (les poules n'ont pas de dents) alors (il fait beau)) »

¬p ⇒ (q ⇒ q). Principe d'explosion Du faux découle n'importe quoi (ex contradictione sequitur quodlibet) (2).
« si (il pleut) alors (je vais au cinéma) » et « si (il pleut) alors (je ne vais pas au cinéma) » sont également vraies un jour de beau temps.

p ⇒ (q ∨ ¬q). La disjonction est toujours vraie.

(p ⇒ q) ∨ (q ⇒ p). Si q est vrai alors (p ⇒ q), si q est faux alors (q ⇒ p).
« (si (je suis vivant) alors (il pleut)) ou (si (il ne pleut pas) alors (je suis vivant)) » est vraie mais aussi « (si (je reste chez moi) alors (je vais à Paris)) ou (si (je ne vais pas à Paris) alors (je reste chez moi)) ».

¬(p ⇒ q) ⇒ (p ∧ ¬q). Si p n'implique pas q alors p est vrai et q est faux.

(1) - Russell

Si 2 + 2 = 5 alors 1 = 2 (on soustrait 3)

2 = 1 (par symétrie)

Comme Moi + Le Pape ça fait 2 et que 2 = 1

je suis Le Pape

(2) - Principe d'explosion
Le faux est donné par deux propositions contradictoires qu'on pose vraies

Soit p et ¬p
(p ∨ q) (*) est vrai (quel que soit q puisque p est vrai)
or ¬p est vrai (hypothèses)
donc q est vrai (puisque (*) est vrai)

Remarques :

- Clarence Irving Lewis proposa de remplacer l'implication matérielle par une implication stricte telle que d'une prémisse fausse ne puisse pas découler une conséquence vraie. Cette proposition est développée dans d'autres logiques.

- La logique formelle n'intègre pas les énoncés contingents. « si n est divisible par 7 alors n est impair » n'a pas de sens mathématique car il manque un quantificateur pour n.

Modus Ponens et Modus Tollens

Le modus ponens (détachement) est une règle primitive du raisonnement logique qui consiste à affirmer une implication « si p alors q », à poser son antécédent « or p » et à en déduire le conséquent « donc q ».

Son étymologie est modus ponendo ponens « manière de poser en posant ».

Écriture formelle : p ⇒ q, p

q qui se lit « de p implique q et de p, on déduit q ».

Le modus tollens (contraposition) est une règle du raisonnement logique qui consiste à affirmer une implication « si p alors q », à nier le conséquent « or non q » et à en déduire la négation de l'antécédent « donc non p ».

Son étymologie est modus tollendo tollens « manière d'enlever en enlevant ».

Écriture formelle : p ⇒ q, ¬ q

¬ p qui se lit « de p implique q et de non q, on déduit non p ».

Condition nécessaire - Condition suffisante

- Si (p ⇒ q), p est une condition suffisante de q, q est une condition nécessaire de p.

- La contraposée de (p ⇒ q) est (¬ q ⇒ ¬ p).

Le modus tollens est l'application du modus ponens à la contraposée d'une implication.

- Ne pas confondre contraposée et réciproque ! (p ⇒ q) est équivalent à (¬ q ⇒ ¬ p) mais pas à la réciproque (q ⇒ p) ni à la négation de l'antécédent (¬ p ⇒ ¬ q) qui est la contraposée de la réciproque.

Raisonnement par l'absurde (reductio ad absurdum) ou apagogie

Il consiste à montrer la vérité d'une proposition en prouvant l'absurdité de la proposition contraire ou à montrer la fausseté d'une proposition en déduisant de sa vérité des conséquences absurdes.

Soit S les axiomes de base et p la proposition à démontrer

Si S∪{¬p}

Faux alors S

p « Si la négation de p dans le contexte S conduit à une contradiction logique, on peut conclure que p se déduit de S »
Remarques :

- « non p faux implique p ». Cette utilisation du Tiers exclu (élimination de la double négation) n'est pas admise en logique intuitionniste.

- « p faux implique non p » n'utilise pas la simplification de la double négation mais la négation simple.
Exemple : Irrationnalité de √2.

Soit p la proposition « √2 est un nombre rationnel »

p ⇒ il existe deux entiers positifs a et b premiers entre eux tels que a / b = √2 ⇔ a² / b² = 2 ⇔ a² = 2b² (1)

⇒ a² pair ⇒ a pair

a pair ⇒ il existe un entier positif c tel que a = 2c ⇔ a² = 4c² (2)

(1) et (2) ⇒ 2b² = 4c² ⇔ b² = 2c²

⇒ b² pair ⇒ b pair

a pair et b pair ⇒ a et b ne sont pas premiers entre eux ⇒ p faux

Donc « √2 n'est pas un nombre rationnel »
L'utilisation d'un raisonnement par l'absurde n'est jamais la seule solution mais il est souvent plus compréhensible que d'autres méthodes susceptibles de donner le même résultat (passage par la contraposée par exemple).

Syllogismes

Ancêtre de la logique moderne, la syllogisme a été formalisé par Aristote.

Il consiste à tirer une conclusion de deux propositions appelées prémisses.

[(M⊂P)∧(S⊂M)]⇒(S⊂P) « M est P or S est M donc S est P »
Exemple classique :

Premisse majeure	Terme moyen (sujet)	copule	Terme majeur (prédicat)
Premisse majeure	Tous les Hommes	sont	mortels
or
Premisse mineure	Terme mineur (sujet)	copule	Terme moyen (prédicat)
Premisse mineure	Tous les Grecs	sont	des hommes
donc
Conclusion	Terme mineur (sujet)	copule	Terme majeur (prédicat)
Conclusion	Tous les Grecs	sont	mortels

Les propositions sont réparties en quatre classes (désignées par des lettres depuis le Moyen-Âge)
Classe	Qualité	Portée du sujet	Portée du prédicat	Expression	Carré logique
A (Affirmo)	Affirmation universelle	Universelle	Particulière	Tous sont...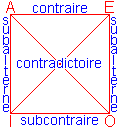
E (nEgo)	Négation universelle	Universelle	Universelle	Aucun n'est...
I (affIrmo)	Affirmation particulière	Particulière	Particulière	Au moins un est...
O (negO)	Négation particulière	Particulière	Universelle	Au moins un n'est pas...

Remarques :

- Des propositions contraires ou subcontraires diffèrent par la qualité (affirmative/négative).

- Des propositions subalternes différent par la quantité (universelle/particulière).

- Des propositions contradictoires diffèrent par la qualité et la quantité.

- Tous les Grecs sont mortels ne signifie pas Tous les mortels sont Grecs alors que Aucun Grec n'est immortel est équivalent à Aucun immortel n'est Grec.

Les syllogismes sont répartis en quatre figures selon la position du terme moyen
Numéro de figure	Forme	Expression
Première	(M⊂P)∧(S⊂M)	M est P or S est M
Deuxième	(P⊂M)∧(S⊂M)	P est M or S est M
Troisième	(M⊂P)∧(M⊂S)	M est P or M est S
Quatrième	(P⊂M)∧(M⊂S)	P est M or M est S

Chacune des trois propositions d'un syllogisme peut appartenir à quatre classes. Compte tenu des quatre figures du moyen terme, 256 syllogismes sont possibles mais seulement 24 d'entre eux sont valides ou concluants.
Historiquement, ils sont identifiés par un mot composé à partir des trois voyelles qui représentent les classes utilisées. Ainsi celui qui est donné en exemple au début est bArbArA pour ses trois Affirmations universelles.

Modes concluants
Figure	Modes
Première : Le Terme moyen est relié à P or S est relié au Terme moyen donc S est relié à P...	bArbArA	cElArEnt	dArII	fErIO	bArbArI	cElArOnt
Deuxième : P est relié au Terme moyen or S est relié au Terme moyen donc...	cEsArE	cAmEstrEs	fEstInO	bArOcO	cEsArO	cAmEstrOs
Troisième : Le Terme moyen est relié à P or le Terme moyen est relié à S donc...	dAtIsI	dIsAmIs	fErIsOn	bOcArdO	fElAptOn	dArAptI
Quatrième : P est relié au Terme moyen or le Terme moyen est relié à S donc...	cAmEnEs	dImAtIs	frEsIsOn	cAlEmOs	fEsApO	bAmAlIp

Remarques :

- Les 24 syllogismes concluants peuvent être réduits aux quatre premiers modes de la première figure (bArbArA cElArEnt dArII fErIO). Ils sont dits parfaits.

Une image et du texte

- L'initiale du nom de chaque mode rappelle le mode parfait auquel il peut être réduit.

- Les lettres qui suivent les voyelles indiquent le type de la transformation à utiliser.

- s derrière un E transforme une universelle négative en universelle négative équivalente « nul X n'est Y ⇒ nul Y n'est X ».

- s derrière un I transforme une particulière affirmative en particulière affirmative équivalente « quelque X est Y ⇒ quelque Y est X ».

- p derrière un A transforme une universelle affirmative en particulière affirmative « tout X est Y ⇒ quelque Y est X ».

- p derrière un I montre que la conclusion particulière « quelque Y est X » vient d'une conclusion universelle « tout S est Y ».

- m permute les deux prémisses.

- c montre qu'un raisonnement par l'absurde sur la conclusion conduit à une contradiction de la prémisse qui précède.
Exemple : Réduction de cAmEstrEs « (1) tout P est M or (2) nul S n'est M donc (3) nul S n'est P ».

- On peut le ramener à cElArEnt (1) nul M n'est P or (2) tout S est M donc (3) nul S n'est P.

- Transformation de (2) en nul M n'est S.

- Permutation des deux prémisses. cElArEnt donne nul P n'est S.

- Transformation simple de la conclusion en nul S n'est P.
Validité d'un syllogisme :

- L'étendue des termes de la conclusion ne peut pas être plus importante que dans les prémisses.

- La conclusion doit être aussi faible que la prémisse la plus faible (particulier < universel, négatif < affirmatif).

- Le moyen terme doit être au moins une fois universel.

- Deux prémisses particulières ne permettent pas une conclusion.

- Deux prémisses négatives ne permettent pas une conclusion.
Remarques :

- Tout syllogisme peut être suspecté car sa validité repose sur des prémisses dont la propre validité n'est généralement pas démontrée.

- Un sophisme est un raisonnement volontairement trompeur. Il peut prendre l'apparence d'un syllogisme en s'appuyant sur des prémisses insuffisantes.

Tout ce qui est rare est cher

Or Un bon cheval à bon marché est rare

Donc Un bon cheval à bon marché est cher. (bArbArA)

- Un paralogisme est un raisonnement faux qui présente une apparence de vérité.

Tout homme est mortel

Or Tout animal est mortel

Donc Tout animal est un homme. (bArbArA)

Exemples de propositions :
2 + 2 = 5	Il pleut sur Nantes.	Je suis plus grand que toi.	Cette feuille est blanche.

Mais pas :
3,14159	Il va pleuvoir.	Je suis beau.	Donne-moi ce livre !

Je mange du fromage.	mange(Je, fromage)	x est pair	est pair(x)
12 < 4	est plus petit(12, 4)	Abel est le frère de Caïn	est frère de(Abel, Caïn)